Distributions again

Let’s briefly revisit the general topic of distributions. Numerically speaking, a distribution is the number of observations per each value of a variable. We could ask our sample whether they like cats, dogs, both, or neither and the resulting numbers would be the distribution of the “pet person” variable (or some other name).

Inspecting a variable’s distribution gives information about which values occur more often and which less often.

We can visualise a distribution as the shape formed by the bars of a bar chart/histogram.

df <- tibble(eye_col = sample(c("Brown", "Blue", "Green", "Gray"), 555,
                        replace = T, prob = c(.55, .39, .04, .02)),
             age = rnorm(length(eye_col), 20, .65))

p1 <- df %>%
  ggplot(aes(x = eye_col)) +
  geom_bar(fill = c("skyblue4", "chocolate4", "slategray", "olivedrab"), colour=NA) +
  labs(x = "Eye colour", y = "Count")

p2 <- df %>%
  ggplot(aes(x = age)) +
  geom_histogram() +
  stat_density(aes(y = ..density.. * 80), geom = "line", color = theme_col, lwd = 1) +
  labs(x = "Age (years)", y = "Count")
  
plot_grid(p1, p2)

Figure 1: Visualising distributions using a bar chart for a discrete variable (eye colour) and a histogram for a continuous variable (age)

Known distributions

As you can imagine, there are all sorts of distributions of various shapes. Some of these shapes can be very accurately described by mathematical functions, or formulae. If there is a formula to draw the line corresponding to the distribution, we say that these distributions are “algebraically tractable”.

Having a formula for a distribution is very convenient because that means, we can derive useful properties of such distributions. For example, we can relatively easily calculate the probability of randomly drawing a number between let’s say 100 and 107 from some distribution. Since statistics is all about probability, you can imagine that this is very handy!

Here are a few examples of mathematical functions that describe known distributions:

df <- tibble(x = seq(0, 10, length.out = 100),
             norm = dnorm(scale(x), sd = .5),
             chi = dchisq(x, df = 2) * 2,
             t = dt(scale(x), 5, .5),
             beta = (dbeta(x / 10, .5, .5) / 4) - .15)

cols <- c("#E69F00", "#56B4E9", "#009E73", "#CC79A7")
df %>%
  ggplot(aes(x = x)) +
  geom_line(aes(y = norm), color = cols[1], lwd = 1) +
  geom_line(aes(y = chi), color = cols[2], lwd = 1) +
  geom_line(aes(y = t), color = cols[3], lwd = 1) +
  geom_line(aes(y = beta), color = cols[4], lwd = 1) +
  labs(x = "x", y = "Density")

Figure 2: Examples from families of known distributions. Yellow - normal distribution; Pink - one of the β-family; Blue - one of the χ²-family; Green - one of the t-family.

We will encounter a few of these distributions along the way to stats enlightenment (t, \(\chi^2\), and F to be precise). But for now, let’s remind ourselves of probably the most important distribution of them all, the normal distribution.

The normal distribution

The normal distribution is fundamental to the kinds of statistics we will be learning and so its crucial that you understand its properties. You may also come across its alternative name, the Gaussian distribution, named after the German mathematician and a notable dead white dude, Carl Friedrich Gauss. Sometimes it’s also referred to as the bell curve due to its symmetrical, bell-like shape but there are other distribution with very similar shapes so maybe let’s not call it that.

Last term we learned about how this distribution arises as a result of additive processes and how this distribution is a function of two parameters: \(\mu\) (mean) and \(\sigma\) (standard deviation). We talked about how changing the mean of the distribution shifts its centre along the x-axis (centring) and how changing the SD determines the spread of the curve (scaling).

Because the normal distribution is symmetrical and bell-shaped, it’s necessarily true that its mean equals its median and its mode.

Now, it’s important to understand that not every symmetrical bell-shaped distribution is normal. To understand what makes a normal distribution normal, we need to understand the concept of area below the curve.

Area below the normal curve

All the functions that draw the various distributions are probability functions, which means that, when plotted on a graph, the y (vertical) coordinate of the curve has to do with probability of observing the corresponding value on the x-axis.¹

Because the probability of getting any value whatsoever when sampling from a distribution is 100% (or 1) – in other words, we will get some value though we don’t know what it will be – the combined area below the curve of a probability distribution is always 1.

We know that the normal distribution is symmetrical about its mean and so the area to the left of \(\mu\) will be the same as the area to the right of it: 0.5, or 50%. So if we were to draw a random observation from a normally distributed variable, we would have a 50% chance of getting a value that’s below the average value and a 50% of getting a value that’s larger than that.

Since the normal distribution is algebraically tractable (i.e., there’s a formula for it), we can use maths² to calculate the are between any two points along the x-axis. This are is always smaller or equal to 1 and will corresponds to the probability of randomly sampling an observation from the distribution whose value lies between these two points.

Now that we know the idea between calculating the probability of a range of values in a given distribution, we are ready to talk about what makes a bell-shaped symmetrical curve normal. The important thing is to understand that it is the particular proportions of the curve that matter, rather than a vague bell-like shape. Take for instance Figure 3 below: Only the left-hand-side curve is normal. The other line, while very similar isn’t a graph of a normal distribution³ (check the code if you don’t believe that they are actually different).

df <- tibble(x = seq(-4, 4, length.out = 100),
             norm = dnorm(x),
             t = dt(x, 6))

p1 <- df %>%
  ggplot(aes(x = x)) +
  geom_line(aes(y = norm), lwd = 1, colour=theme_col) +
  labs(x = "x", y = "Density")
p2 <- df %>%
  ggplot(aes(x = x)) +
  geom_line(aes(y = t), lwd = 1, colour=second_col) +
  labs(x = "x")

plot_grid(p1, p2)

Figure 3: Even though these two curves look very similar, the right-hand side one is not normal because it’s proportions are slightly off

Here is a visualisation of these proportions:

quantiles <- tibble(x1 = -(1:3), x2 = 1:3, y = c(.21, .12, .03))
tibble(x = seq(-4, 4, by = .1), y = dnorm(x, 0, 1)) %>%
  ggplot(aes(x, y)) +
  geom_density(stat = "identity", color = default_col) +
  geom_density(data = ~ subset(.x, x <= quantiles$x1[3]),
               stat = "identity", color = default_col, fill = default_col) +
  geom_density(data = ~ subset(.x, x >= quantiles$x2[3]),
               stat = "identity", color = default_col, fill = default_col) +
  geom_density(data = ~ subset(.x, x >= quantiles$x1[2] & x <= quantiles$x2[2]),
               stat = "identity", color = NA, fill = second_col) +
  geom_density(data = ~ subset(.x, x >= quantiles$x1[1] & x <= quantiles$x2[1]),
               stat = "identity", color = NA, fill = theme_col) +
  geom_segment(data = quantiles,
               aes(x = x1, xend = x2, y = y, yend = y),
               arrow = arrow(length = unit(0.2, "cm"), angle = 15,
                             type = "closed", ends = "both"),
               color = c(bg_col, default_col, default_col)) +
  geom_line(data = tibble(x = rep(c(-1, 1), 2), y = rep(c(.12, .03), each = 2)),
            aes(x, y, group = y), color = bg_col) +
  geom_line(data = tibble(x = rep(c(-(2:3), 2:3), each = 2),
                          y = as.vector(rbind(0, rep(quantiles$y[-1] + .005, 2)))),
            aes(x, y, group = x), lty = 2, color = default_col) +
  annotate("text", x = rep(0, 3), y = quantiles$y + .05,
           label = c("68.2%", "95.4%", "99.7%"), color = bg_col) +
  labs(x = "z-score", y = "Density") +
  scale_x_continuous(breaks = -4:4)

Figure 4: Proportions of area below the normal curve with respect to multiples of σ on either side of the mean

The R know-how box below shows you how to get the proportion of the area below the normal curve between \(\mu−1\sigma\)and \(\mu+1\sigma\). Do check it out!

lower <- pnorm(q = -1,  # -1 sigma from the mean
      mean = 0, # set the mu of the distribution
      sd = 1) # set the sigma of the distribution
lower

[1] 0.1586553

higher <- pnorm(q = 1, mean = 0, sd = 1) # +1 sigma from the mean
higher

[1] 0.8413447

higher - lower

[1] 0.6826895

We can calculate (or let R do it for us) the proportion of the area under the curve for any multiple of SD from the mean of the distribution, or even between any two points along the x-axis.

Conversely, we can reverse the maths to get the value along the x-axis that cuts the distribution into pieces of any proportion. We already learnt that drawing a vertical line down the normal distribution at its mean (e.g., zero SD from the mean) will cut it into lower half and upper half. If we drew this line at \(\mu-1\times\sigma\), we would be cutting the distribution into lower/left 15.87% and upper/right 84.13%.

We can apply the same kind of maths to “chop off” extreme values in a distribution, that is those values that we wouldn’t expect to observe often. Let’s say we want to know the number of _SD_s from the mean beyond which lie the outer 5% of the distribution. Plugging in the numbers, we get around \(\mu\pm1.96\times\sigma\). We can visualise this area like this:

quantiles <- qnorm(.025) * c(-1, 1)
tibble(x = sort(c(quantiles, seq(-4, 4, by = .1))), y = dnorm(x, 0, 1)) %>%
  ggplot(aes(x, y)) +
  geom_line(color = default_col) +
  geom_density(data = ~ subset(.x, x >= quantiles[1]),
               stat = "identity", color = NA, fill = second_col) +
  geom_density(data = ~ subset(.x, x <= quantiles[2]),
               stat = "identity", color = NA, fill = second_col) +
  geom_line(data = tibble(x = rep(quantiles, each = 2),
                          y = c(0, .15, 0, .15)),
            aes(x, y, group = x), lty = 2, color = default_col) +
  geom_segment(data = tibble(x = quantiles, xend = c(4, -4),
                             y = c(.15, .15), yend = c(.15, .15)),
               aes(x = x, xend = xend, y = y, yend = yend),
               arrow = arrow(length = unit(0.2, "cm"),
                             angle = 15, type = "closed"),
               color = default_col) +
  annotate("text", x = c(-2.8, 2.8), y = .18,
           label = ("2.5%"), color = default_col) +
  labs(x = "z-score", y = "Density")

Figure 5: The extreme 5% of the normal distribution (2.5% in the left tale and 2.5% in the right tail) lies outside of ±1.96 SD from the mean

qnorm(p = .025,  # probaility corresponding to the lower 2.5% cut-off
      mean = 0, # set the mu of the distribution
      sd = 1) # set the sigma of the distribution

[1] -1.959964

# upper 2.5% cut-off (97.5% counting from the left-hand-side)
qnorm(p = .975, mean = 0, sd = 1)

[1] 1.959964

Critical values

The principles explained above mean that, if we have a variable that can be reasonably assumed to be normally distributed and if we know its SD, we can calculate these cut-off point (critical value) for any proportion of our data. This is very useful for specifying the criteria for what we consider outliers in out data.

For example, we could say that the most extreme 3% of our data should be considered outliers and removed from our dataset. If we can assume that our data come from a normally distributed population, we can use our sample mean and SD to calculate the critical value that cuts off 1.5% from either tail of the distribution.

Let’s say we asked a sample of people how many grammes of chocolate they eat per week. Let’s also assume that the underlying variable is normal. We looked at the descriptive statistic of the variable and found that the mean grammes consumed is 53.7 with SD = 17.6.

The critical values that cut off bottom and top 1.5% of a normal distribution with a mean of 0 and SD of 1 (AKA the standard normal distribution) are about −2.17 and 2.17, respectively. Multiplying each of these numbers by the SD of our variable, gives us the number of grammes from the mean of the distribution that should be our cut-offs for outliers: ±38.19. That means that we can expect 3% of the population from which we sampled our data to have values smaller than 15.51 and larger than 91.89.

In other words, under our 3% criterion for outliers, we can consider anyone who eats less than 15.51 or more than 91.89 grammes of chocolate per week an outlier (see the R know-how box below for a quick way of getting these numbers).

qnorm(p = .015, mean = 53.7, sd = 17.6) # lowest 1.5%

[1] 15.50641

qnorm(p = .985, mean = 53.7, sd = 17.6) # highest 1.5%

[1] 91.89359

Now that we have a solid understanding of the normal distribution, the area below its curve and of the concept of critical values, we can move on to talking about population parameter estimates. To get there, we first need to revisit a few topics.

Sampling from distributions

As you will recall, when we collect data from participants on some variable, we are assuming that individual observations are sampled randomly from the population. Remember that the term population does not necessarily refer to people. Population is the set of all observations of a given variable.

When it comes to the kind of things we investigate as psychologists using quantitative research, such as traits, abilities, or attitudes, many – though certainly not all – are assumed to come from a normal distribution.

Let’s mention just a few instances where the normal distribution is not a reasonable assumption: Reaction times tend to be reasonably well described by the log-normal distribution, similar to the distribution of wealth we discussed last term. Passes and fails on an exam are distributed according to the binomial binomial distribution, while the number of calls to a call centre within a minute follow the Poisson distribution. The point of these examples is to illustrate that, though distributions are idealised mathematical forms, they can be used to model things in the real world. Every time we’re collecting data on real-life variables, we are essentially sampling from these distributions.

Naturally, any two samples are very likely to be different from one another, even if they originate from the same population. Two bags of Skittles from the same factory will most likely have different distribution of colours because they are produced at random.⁴

The same is the case with any other variable. We can easily demonstrate this by simulating drawing two samples from the same population in R:

# draw a sample of 10 from a normally distributed
# population with mean 100 and sd 15
rnorm(n = 6, mean = 100, sd = 15) 

[1] 101.61958  80.95560  89.62080  96.04378 106.40106  86.21514

# repeat
rnorm(6, 100, 15) 

[1]  80.31573 107.63193  85.82520  99.95288  93.55956  74.73945

As you can see, the numbers in the respective samples are not the same.

Because the values of the observations aren’t the same, the statistics calculated based on two samples will also differ. To illustrate this, let’s ask R to draw two samples of 50 observations each from a normal distribution with mean of 100 and SD of 15 and calculate the means of both of these samples.

sample1 <- rnorm(50, 100, 15)
sample2 <- rnorm(50, 100, 15)

mean(sample1)

[1] 98.56429

mean(sample2)

[1] 105.4175

So the means (\(\bar{x}\)) of our two samples are not equal. What’s also important to understand is that these statistics also very likely to differ from the from the population parameter (e.g., \(\mu\)). In each case, however, the sample mean is our best estimate of the population mean.

p1 <- ggplot(NULL, aes(x = sample1)) +
  geom_histogram(bins = 15) +
  geom_vline(xintercept = mean(sample1), color = second_col, lwd = 1) +
  labs(x = "x", y = "Frequency") + ylim(0, 8)
p2 <- ggplot(NULL, aes(x = sample2)) +
  geom_histogram(bins = 15) +
  geom_vline(xintercept = mean(sample2), color = second_col, lwd = 1) +
  labs(x = "x", y = "") + ylim(0, 8)
plot_grid(p1, p2)

Figure 6: Two samples from the same population differ both in their distributions and, as a result, in their sample statistics, in this case their means (vertical lines).

Sampling distribution

Let’s briefly recap what we learnt about the sampling distribution last term and set it in the context of estimating parameters.

Because we know that the mean (or any other statistic) calculated using our sample is just one of the possible ones and it depends solely on the particular characteristics of the sample, we know that there exists an entire “universe” (or population!) of sample means and the mean we got in our sample represents just one observation of this universe. If we took all possible samples of a given size (let’s say N = 50) from the same population and each time calculated \(\bar{x}\), the means would have their own distribution. This is the sampling distribution of the mean.

Each of these hypothetical sample means can be used as estimates of the population mean – the one true mean of the entire population. Sadly, we can never know its value but we know it exists. We also know that its value is identical to the mean of the sampling distribution. Sadly (there’s a lot of sadness in stats!), we will never observe the entire sampling distribution either as it would require getting all possible samples of a given size from the same population.

But just because we can’t observe the sampling distribution, it doesn’t mean that we don’t know anything about it. In fact, we know its key properties: Its mean is equal to the value of the population parameter and it’s standard deviation, called the standard error, is related to the population standard deviation \(\sigma\) and sample size \(N\):

\[SE = \frac{\sigma}{\sqrt{N}}\]

Now, we don’t know the value of σ for the same reason we don’t know the value of \(\mu\) but we can estimate the standard error from sample standard deviation, \(s\) as:

\[\widehat{SE} = \frac{s}{\sqrt{N}}\]

To illustrate what a sampling distribution may look like, let’s simulate one in R! Imagine we went and bought a big bag of 20 apples. Each apple has its weight. Let’s assume, that the weights are distributed normally and that the population mean \(\mu\) is 173g with a \(\sigma\). The benefit of simulation is that we can just decide what our population parameters are while, in reality, these values are, and will ever, be unknown. We calculate the mean weight of our sample, knowing that it will be just one possible sample means and it will most likely differ from \(\mu\).

Now, imagine we spent the rest of our days going round buying bags of 20 apples until we got 100,000 of them, calculating the sample mean of each bag. Because all these means are based on samples from the same population and of the same size, they come from the same sampling distribution of the mean. We still don’t have the entire distribution but with 100k means, we have a reasonably good approximation.

n <- 20
mu <- 173
sigma <- 23
x_bar <- replicate(100000, mean(rnorm(n, mu, sigma)))
mean(x_bar)

[1] 172.9955

Here’s the distribution of our 100k means visualised:

ggplot(NULL, aes(x_bar)) +
  geom_histogram(bins = 51) +
  geom_vline(xintercept = mean(x_bar), col = second_col, lwd = 1) +
  labs(x = "Sample mean", y = "Frequency") 

Figure 7: Approximation of the sampling distribution of the mean from the example population based on 100,000 simulated samples. Vertical line represents the mean of the distribution.

Notice, that the mean of our “sampling distribution”, 172.99 is pretty close to the population mean, we decided ahead of our simulation (173). If we had the entire sampling distribution, its mean would be actually identical to \(\mu\)!

Standard error

You already know what the standard error is so this will be quick.

Standard error is simply the SD of the sampling distribution. In our simulation example, the distribution of 100k sample means of apple weights had a SD of 5.144. This is very close to the actual SE calculated using the formula:

\[\begin{aligned}SE &= \frac{\sigma}{\sqrt{N}}\\ &= \frac{23}{\sqrt{20}}\\ &\approx 5.1429563\end{aligned}\]

# based on simulated sampling dist
sd(x_bar)

[1] 5.15595

# based on set population parameters
se <- 23/sqrt(20)
se

[1] 5.142956

As we said above, we don’t really have access to the entire sampling distribution (not even the miserly 100k samples!) or the population parameters and so we have to estimate SE using the standard deviation of our actual sample.

Let’s use R to draw a single sample (N=20) from our population of apples and estimate the value of SE on the basis of it:

samp <- rnorm(n, mu, sigma)
# SE-hat
se_hat <- sd(samp)/sqrt(length(samp))
se_hat

[1] 4.894174

# compare to actual SE
se

[1] 5.142956

As you can see, our \(\widehat{SE}\) of 4.894 is a bit of an overestimate compared to the actual \(SE\) of 5.143. That’s just what happens with estimates, they’re often close but almost never precise.

OK, so what is the standard error actually for? What does it tell us?

The smaller the SE, the more confident we can be that the parameter estimate (\(\hat{\mu}\)) in our sample is close to those in other samples of the same size.

Now, because SE is calculated using N, there is a relationship between the two:

Figure 8: Magnitude of SE is a function of sample size: Given a constant SD, SE gets smaller as N gets larger

That is why larger samples are more reliable!

Understanding sampling distributions and their properties prepares the ground for exploring a key principle in statistics…

The Central Limit Theorem

This core principle in statistics is named “central” because of how important it is to statistics but, once you understand the sampling distribution, it’s really rather simple. It’s actually the simplicity that makes its importance so impressive.

By approximately normal we mean that as the sample size that characterises the sampling distribution get larger, the shape of the sampling distribution approaches normal. That’s pretty much all there is to the Central Limit Theorem so make sure you understand these two statements.

Actually, we already demonstrated the CLT last term, though we didn’t refer to it by its name.

Let’s see how the CLT applies to the sampling distribution of estimates of the mean based on samples form a non-normal population. In the top plot of animation below, we repeatedly draw samples of N = 20. The green area is the underlying distribution of the population and, as you can see, it’s resolutely not normal.

Every time we pick a sample, we calculate it’s mean and plot it on a histogram in the bottom panel. The blueish shape is the sampling distribution of the mean based on N = 20 so that’s the shape we’re expecting to eventually get.

As you can see that’s kind of the shape our histogram of sample means forms. It’s not exactly the same because we are drawing a relatively small number of samples (about 10k) but if we were to continue, the shape would get smoother.

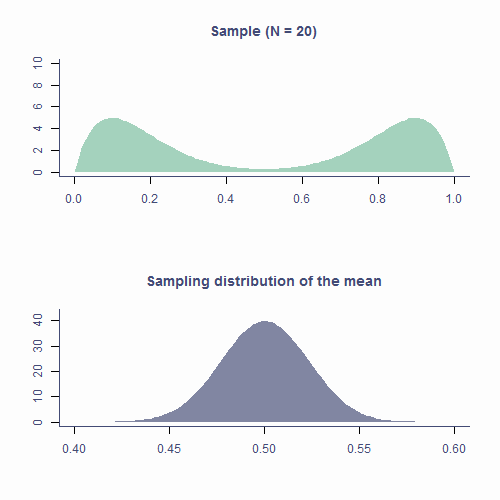
Approximately normal

OK, so that’s one of the parts of the CLT – the sampling distribution of the mean will be normal even if the underlying population distribution is not. But what about “approximately” normal? How does that work.

To see this, let’s simulate sampling distributions (100k means) from the same population based on N = 5, N = 30, and N = 1,000 and plot them on histograms:

par(mfrow=c(2, 2), mar = c(3.1, 4.1, 3.1, 2.1), cex.main = 2)
pop <- tibble(x = runif(100000, 0, 1)) %>%
  ggplot(aes(x)) +
  geom_histogram(bins = 25) +
  geom_vline(aes(xintercept = mean(x)), lwd = 1, color = second_col) +
  labs(title = "Population", x = "", y = "Frequency")

plots <- list()
n <- c(5, 30, 1000)
ylab <- c("", "Frequency", "")
for (i in 1:3) {
plot_tib <- tibble(x = replicate(1000, mean(runif(n[i], 0, 1))))
plots[[i]] <- ggplot(plot_tib, aes(x)) +
  geom_histogram(aes(y = ..density..), bins = 30) +
  labs(title = bquote(paste(
    italic(N)==.(n[i]),
    "; ",
    italic(SE)==.(round(sd(plot_tib$x), 2)))),
    x = "", y = ylab[i]) +
  # xlim(0:1) +
  stat_density(geom = "line", color = second_col, lwd = 1)
}

plot_grid(pop, plots[[1]], plots[[2]], plots[[3]])

Notice that, as N gets larger, the sampling distribution of \(\mu\) tends towards a normal distribution with mean = \(\mu\) and \(SD=\frac{\sigma}{\sqrt{N}}\).

If we disregard the word “approximately” for a wee bit, and say that the sampling distribution of the mean is normal, we’ll realise that everything that applies to the normal distribution applies to the sampling distribution of the mean: ~68.2% of means of samples of size 50 from this population will be within ±5.14 of the true mean. And if ~68.2% of sample means lie within ±5.41, then there’s a ~68.2% probability that \(\bar{x}\) will be within ±5.41 of \(\mu\)!

The last paragraph takes a while to wrap ones head around so spend some time on it.

As a matter of convention, in practice, we tend to assume that the sampling distribution is normal when the sample size is larger than 30. We will talk about the reason for this next time but for now, that’s plenty…